Two-Level Segregated Fit Memory Allocator
Last week, I decided to develop a simple memory allocator for Vulkan. Initially, it was meant to be a quick combination of a pool allocator and a free-list allocator (with the free-list backed by pools of memory). However, I was not satisfied with it and started looking into improving my allocator which led me to a paper titled “TLSF: a New Dynamic Memory Allocator for Real-Time Systems”. So here we are.
Introduction
The most basic data structure for memory allocation is free-list. As the name suggests, it involves maintaining a linked list of free memory blocks. Depending on our strategy (first-fit, best-fit, good-fit), we traverse through the linked list to find a suitable block for a memory allocation. While being very simple to implement, the approach often results in an O(N) runtime. While this might not be a problem for most applications, it’s a different story for embedded or real-time systems.
Two-Level Segregated Fit (TLSF)
The TLSF memory allocation algorithm provides O(1) memory allocation and deallocation with a good-fit strategy. TSFL utilizes a two-level segregated data structure to optimize lookup on the freelist. Like many data structures in computer science, fast lookup is achieved through binning or bucketing.
The basic idea is to have M blocks or bins, each of which is further divided in N blocks or sub-bins. These sub-bins then store our free lists.
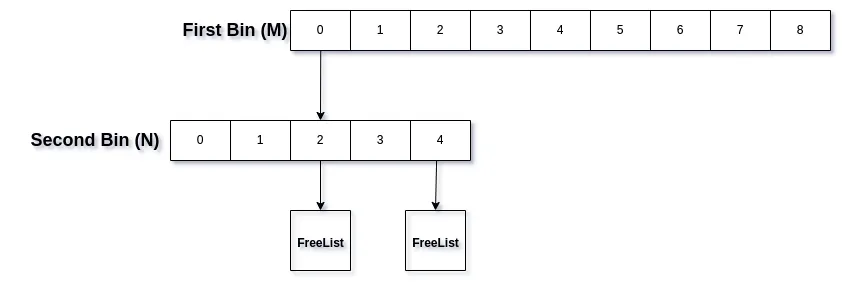
To determine the bin sizes, we follow a specific approach. The idea is to arrange first bins in intervals of power of two (2bin_idx) and then each bin is further divided into M subbins, with the subbin division being linear.
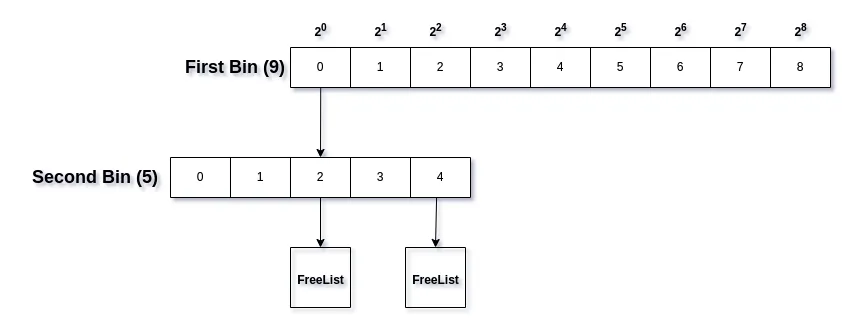
For example, free memory blocks with size in the range [24, 25) will be placed inside bin with index 4. To determine the subbin index, we can take the block size, subtract it with 2bin_idx and divide it by bin_interval / subbin_count.
Given the memory size, we can compute bin and subbin index with:
With this, we know where to store or find memory blocks given their size. But how do we determine which bin and subbins have free memory to allocate from? For this, we can use a lookup table that maps the bin index to a boolean value indicating whether it’s free or not. This can be easily implemented as a bitset. We’ll need a bitset for the first-level bin and bitsets for each subbin under each bin.
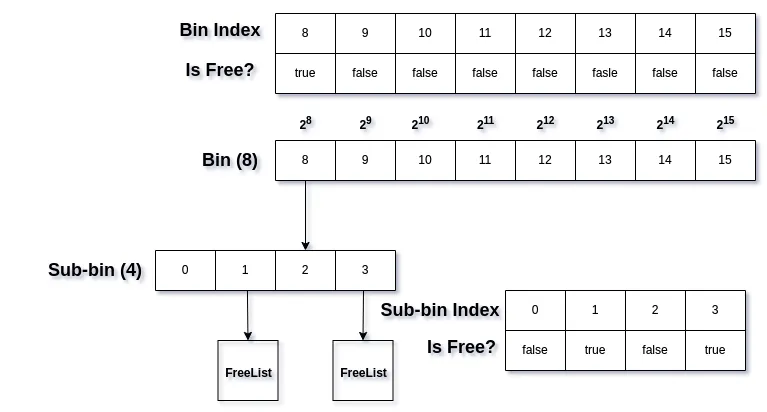With this our datastructure is nearly complete. All that remains is to slove a minor edge case.
In the first-level bin, the starting bin intervals are very small (20, 21, 22, …). Since they can only be used to bin a very small set of sizes, we can just opimize them by making first bin with index 0 a linear or fixed-size bin and using it for all small allocations.
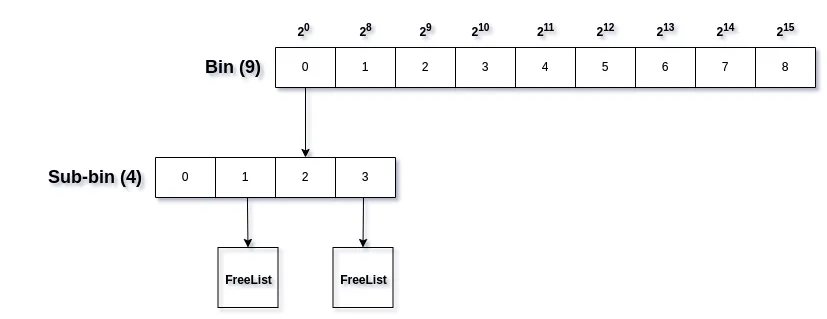As you can see, the first bin looks different. Now, the first bin has a fixed size 27, and our second bin starts from 28 interval. This also implies that we’ll need to subtract our bin index with this fixed size in order to compute actual bin index.
First, we define our fixed linear interval (Linear), and then we compute our bin and sub-bin index accordingly.
This ensures that all blocks in the range [2^0, 2^7) exist in bin 0, and the range [2^7, …) starts from bin 1. With these adjustments, we are ready to implement our own TLSF allocator.
Implementation Details
Some Zig code snippets for implementing a TLSF allocator. Let’s start by defining our constants:
const linear: u8 = 7; // log2(min_allocaction_size)
const sub_bin: u8 = 5; // log2(sub_bin_count)
const bin_count: u32 = 64 - linear; // 64 first level bins
const sub_bin_count: u32 = 1 << sub_bin;
const min_alloc_size: u32 = 1 << linear;
Bin Mapping
We need to map allocation and memory block sizes to proper bin and subbin indices. Two types of mapping are required here: map up and map down. Whenever we what to perform a search for free blocks in order to allocate memory, we would need to map up, which is achieved by rounding up the size to the next subbin. This is necessary because we need to look for a subbin which contains blocks that can at least fit the requested size.
fn binmap_up(size: vk.DeviceSize) BlockMap {
const bin_idx: u32 = bit_scan_msb(size | min_alloc_size);
const log2_subbin_size: u6 = @intCast(bin_idx - sub_bin);
const next_subbin_offset = (@as(u64, 1) << (log2_subbin_size)) - 1; // block_size - 1
const rounded = size +% next_subbin_offset;
const sub_bin_idx = rounded >> log2_subbin_size; // rounded_size / block_size
const adjusted_bin_idx: u32 = @intCast((bin_idx - linear) + (sub_bin_idx >> sub_bin)); // adjust bin_idx with linear
const adjusted_sub_bin_idx: u32 = @intCast(sub_bin_idx & (sub_bin_count - 1)); // sub_bin_idx % sub_bin_count
const rounded_size = (rounded) & ~next_subbin_offset;
std.debug.assert(adjusted_bin_idx < bin_count);
std.debug.assert(adjusted_sub_bin_idx < sub_bin_count);
return .{
.bin_idx = adjusted_bin_idx,
.sub_bin_idx = adjusted_sub_bin_idx,
.rounded_size = rounded_size,
};
}
And for other operations like inserting new free block, we’ll map down.
fn binmap_down(size: vk.DeviceSize) BlockMap {
const bin_idx: u32 = bit_scan_msb(size | min_alloc_size);
const log2_subbin_size: u6 = @intCast(bin_idx - sub_bin);
const sub_bin_idx = size >> log2_subbin_size; // size / block_size
const adjusted_bin_idx: u32 = @intCast((bin_idx - linear) + (sub_bin_idx >> sub_bin));
const adjusted_sub_bin_idx: u32 = @intCast(sub_bin_idx & (sub_bin_count - 1));
const rounded_size = size;
std.debug.assert(adjusted_bin_idx < bin_count);
std.debug.assert(adjusted_sub_bin_idx < sub_bin_count);
return .{
.bin_idx = adjusted_bin_idx,
.sub_bin_idx = adjusted_sub_bin_idx,
.rounded_size = rounded_size,
};
}
Free Block Lookup
// bit sets for our lookup table
bin_bitmap: u32,
sub_bin_bitmap: [bin_count]u32,
We first map the input size to bin and subbin indices and then perform a lookup on the bitsets to check whether the mapped bin and subbin have free blocks or not. If not, we lookup the next free bin, which by default will be large enough.
fn findFreeBlock(self: TSFLAllocator, size: vk.DeviceSize) !BlockMap {
var map = binmap_up(size);
// look up with mapped bin and sub_bin
var sub_bin_bitmap = self.sub_bin_bitmap[map.bin_idx] & (~@as(u32, 0) << @intCast(map.sub_bin_idx));
// not found
if (sub_bin_bitmap == 0) {
// search for next free bin
const bin_bitmap = self.bin_bitmap & (~@as(u32, 0) << @intCast(map.bin_idx + 1));
// no free bins
if (bin_bitmap == 0) return error.OutOfFreeBlock;
// convert bitset flag to bin index
map.bin_idx = @ctz(bin_bitmap);
// any subbin will suffice
sub_bin_bitmap = self.sub_bin_bitmap[map.bin_idx];
}
// get index of free block
map.sub_bin_idx = @ctz(sub_bin_bitmap);
return BlockMap{
.bin_idx = map.bin_idx,
.sub_bin_idx = map.sub_bin_idx,
.rounded_size = map.rounded_size,
};
}
Insert or Remove Block
Whenever we insert or remove a free block from our TSFL structure, we’ll need to update the lookup table aswell.
fn insertFreeBlock(self: *TSFLAllocator, block: *Block) void {
const map = binmap_down(block.size);
//////////////////////////////////////////////////////
// You'd be updating your freelist here
//////////////////////////////////////////////////////
// set bin and subbin bitset
self.bin_bitmap |= @as(u32, 1) << @intCast(map.bin_idx);
self.sub_bin_bitmap[map.bin_idx] |= @as(u32, 1) << @intCast(map.sub_bin_idx);
}
Good-fit
Since we are rounding up the size to the next subbin during free block lookup, TLSF will try to return the smallest chunk of memory big enough to hold the requested block. This makes the algorithm almost best-fit but not exactly best-fit, also called good-fit.
Wrap-Up
And that’s it, everything from here on would involve managing the freelist that are associated with our subbins. Since the operations for searching, inserting and removing are now O(1) with the help of our fast bitset lookup, the resulting allocation or free operation is also O(1). This kind of binning algorithm has multiple use cases, with optimizing memory allocation being one of them.