Sparse Set - flexible cache friendy data structure

The first time I heard about a sparse data structure (specifically, sparse arrays) was in a computer science class. Back then, I didn’t think much of them and didn’t encounter them again until recent years. I’ve been working a lot with contiguous memory and dynamic arrays. While dynamic arrays are extremely cache-friendly and allow code to take advantage of the spatial locality of the CPU cache, operating on them often gets quite tricky. Lets jump into the problems with plain dynamic arrays first.

The problem

Arrays have O(1) access time, but only when the indices are stable. Maintaining a stable index for an element in an array can be challenging, especially when we continuously add and remove elements. If we could maintain stable indices, we could use the index as a key or pointer to the element in the array without relying on other cache inefficient data structures like linked lists or hashmaps. This key would remain valid even when the length of the array changes.

Stable indices here mean that the index of an element in an array does not change when other elements are added or removed from the array.

Sparse Set

Sparse set solves the issue of stable indices with the help of two arrays: one for the indices (sparse) and the other for the actual data (dense). The basic idea is to use the index of the sparse array as a stable index; the element at that index in the sparse array holds the index of an element in the dense array where the actual data is stored.

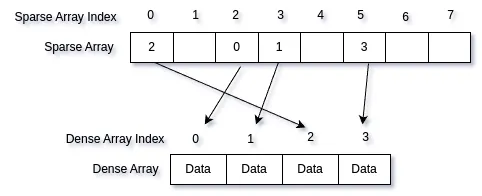
As shown in the diagram above, the sparse array stores indices pointing to elements in the dense array where the actual data is stored. With this mapping, we can easily update the dense array without losing index stability.

If we were to remove the element with index 3 (sparse index), we could simply perform a swap-remove in the corresponding dense array and update the appropriate indices in the sparse array.

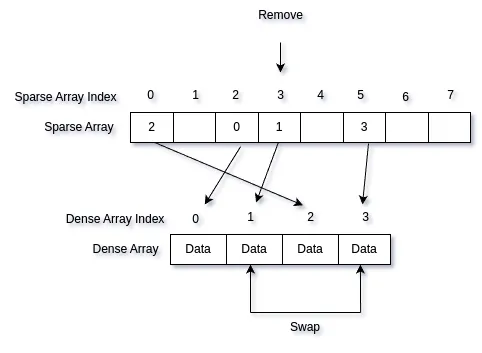
After swapping the elements in the dense array, we would then update the corresponding indices in the sparse array. Sparse index 5 now points to dense index 1, and sparse index 3 points to dense index 3.

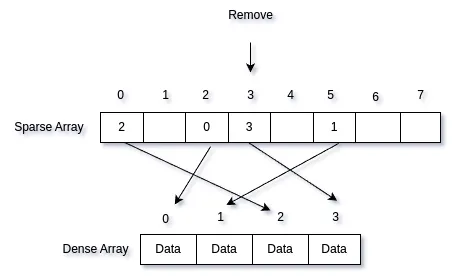
Finally, just pop the element from the dense array.

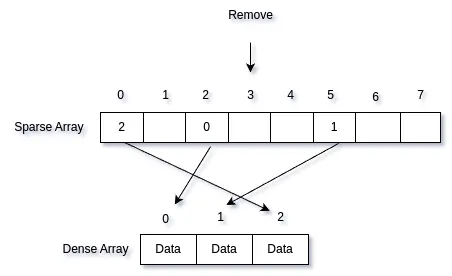
This way, the actual index of the element, which is the sparse index, remains stable.

Implementation

Now that we have the basic idea behind sparse arrays, let’s look at a proper implementation.

template <typename T>
struct SparseSet {
    struct DenseElement {
        size_t sparse_idx;
        T value;
    };

    size_t size = 0;
    std::vector<size_t> sparse;
    std::vector<DenseElement> dense;

    size_t add(T item) {
        auto dense_idx = this->size;
        this->size += 1;

        // try to reuse last freed index
        if(dense_idx < this->dense.size()) {
           auto dense_element = &this->dense[dense_idx];
           dense_element->value = item;
           return dense_element->sparse_idx;
        }

        // allocate new index
        auto sparse_idx = this->sparse.size();

        this->dense.push_back({sparse_idx, item});
        this->sparse.push_back(dense_idx);

        return sparse_idx;
    }

    bool remove(size_t idx) {
        if(!contains(idx)) return false;
        this->size -= 1;

        auto dense_idx = this->sparse[idx];
        auto end_dense_idx = this->size;

        // swap remove
        auto end_element = this->dense[end_dense_idx];
        this->dense[dense_idx] = end_element;
        this->sparse[end_element.sparse_idx] = dense_idx;

        // update end dense idx for reuse
        this->dense[end_dense_idx].sparse_idx = idx;
        this->sparse[idx] = end_dense_idx;

        return true;
    }

    std::optional<T*const> getPtr(size_t idx) {
        if(!contains(idx)) return std::nullopt;

        return {&this->dense[this->sparse[idx]].value};
    }

    bool contains(size_t idx) {
        if(idx >= this->sparse.size()) return false;
        auto dense_idx = this->sparse[idx];
        auto current_idx = this->dense[dense_idx].sparse_idx;
        return dense_idx < this->size && idx == current_idx;
    }

    std::pair<typename std::vector<DenseElement>::const_iterator, 
        typename std::vector<DenseElement>::const_iterator>
    iterator() {
        auto start = this->dense.begin();
        auto end = this->dense.begin() + this->size;
        return { start, end };
    }
};

Complete Implementation on Compiler Explorer

Stable Pointers

Stable indices are useful, but we can also achieve stable pointers for elements in the sparse set. The second part of this post goes into the details of implementing a sparse set with stable pointers. Link to the post

Wrap-up

The sparse set is a useful data structure that combines the benefits of an array with stable indices and stable pointers (details in the next article). The major downside of a sparse set is that it uses more memory, as we maintain a sparse array, which isn’t particularly memory-efficient. Like most algorithms in computer science, this is a trade-off that can be really useful in many scenarios.

References

• Flecs